Tanım

Soyut olarak yöneyler, bir F cisminin üzerine tanımlı bir yöney uzayının öğeleridir. Yöneyler bu cisim üzerine tanımlanmış bir denklik bağıntısı yardımıyla tanımlanabilir. $a,b,c,d in F^n=F times F times cdots times F$ (n tane) olsun. a öğesi ile b öğesi, ancak bileşenlerin toplamı olarak a+d=b+c ise bağıntılıdır. Daha biçimsel olmak gerekirse

$a sim b Leftrightarrow forall i in {1, 2, cdots, n } : quad a_i+d_i=b_i+c_i$

şeklinde tanımlanır ki burada $a_i in F$ 'ler a noktasının koordinatlarıdır ve + işlemi F cismine aittir.

Bu bağıntının bir denklik bağıntısı olduğu kolaylıkla görülebilir. O halde yöney, denklik sınıflarıdır. Böylece denklik sınıfı temsilcisini koyu harfle gösterirsek, bir yöney

$mathbf{a}={a|a sim b }$

olarak tanımlanmış olur. Daha açık bir biçimde bir yöney,

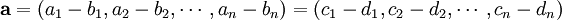
$mathbf{a}=( a_1-b_1,a_2-b_2,cdots,a_n-b_n )=( c_1-d_1,c_2-d_2,cdots,c_n-d_n )$

şeklinde düşünülebilir.

Gösterim

Bir yöney çok çeşitli şekillerde gösterimlenebilir. En yaygın gösterimler, üzerinde bir ok işareti ( $vec{a}$ ) ya da koyu harf ( $mathbf{a}$ ) gösterimidir. Oklu gösterimin avantajı el yazılarında kolaylıkla kullanılabilir olmasıdır. Ancak baskı ve sayısal metinlerde koyu harf kullanmak adettir.

Yöneyin bileşenleriyle gösteriminde ise genellikle sıralı n-li kullanılır.

$mathbf{a}=(a_1,a_2,cdots,a_n)$

Yer yer (konunun veriliş tarzına bağlı olarak) satır ya da sütun dizey gösterimi de yeğlenir.

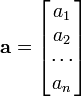
$mathbf{a}=begin{bmatrix}a_1 & a_2 & cdots & a_n end{bmatrix}$ ya da $mathbf{a}=begin{bmatrix}a_1 \ a_2 \ cdots \ a_n end{bmatrix}$

Yine yaygın gösterimlerden biri birim yöney gösterimidir.

$mathbf{a}=a_1 mathbf{i}_1+a_2 mathbf{i}_2+cdots+a_n mathbf{i}_n$

ki burada

$mathbf{i}_1=(1,0,cdots,0)$

$mathbf{i}_2=(0,1,0,cdots,0)$

$vdots$

$mathbf{i}_n=(0,cdots,0,1)$

alınabilir.

Bir yöney

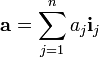
$mathbf{a}=sum_{j=1}^n a_j mathbf{i}_j$

şeklinde düşünüldüğünde Einstein toplam uzlaşımı kullanılarak

$a=a_j mathbf{i}_j quad quad quad (j=1,2,cdots,n)$

şeklinde gösterilebilir. Bu gösterim, toplam simgesinden kurtulmada ve bileşenleri temsil edecek şekilde bir kolaylık sağlamaktadır. Genellikle tensör gösterimi olarak anılır.

Köken

İngilizce'de bu yapı için kullanılan sözcük vector dür. Kökeni, "taşımak"/"bir yöne aktarmak"/"göndermek" anlamına gelen "vehere" Latince fiil gövdesidir^[1]. Sözcüğün anlamı "taşıyıcı"/"yöncü" olarak düşünülebilir. Bu yüzden olabilir ki Türkçe'de (büyük ihtimalle Fransızca'dan devşirilmiş olan) vektör karşılığından sonra yöney karşılığı kullanılmaktadır^[2].

Yöney İşlemleri [değiştir]

Eşitlik

Ancak yöneylerden birinin her bileşeni karşılıklı olarak diğerininkine eşitse bu iki yöney eşittir.

$mathbf{a}=mathbf{b} Leftrightarrow forall a_i,b_i: a_i=b_i$

Daha cebirsel olarak, iki yöney aynı denklik sınıfına aitse eşittir.

Yöney toplamı

İki yöneyin toplamı üçüncü bir yöneye eşittir.

$mathbf{a}+mathbf{b}$	$=(a_1 mathbf{i}_1+a_2 mathbf{i}_2+cdots+a_n mathbf{i}_n)+(b_1 mathbf{i}_1+b_2 mathbf{i}_2+cdots+b_n mathbf{i}_n)$
	$=(a_1+b_1)mathbf{i}_1 + (a_2+b_2)mathbf{i}_2 + cdots + (a_n+b_n)mathbf{i}_n$
	$=begin{bmatrix}a_1+b_1 \ a_2+b_2 \ cdots \ a_3+b_3end{bmatrix}$

Skaler (sayıl) ile çarpımı

Bir yöney uzayında, sayıl ve yöneyler arasında bir çarpma ve dağılma olması gerekir. r,s sayılları F cismine ait olsun. O halde $mathbf{a}$ , $mathbf{b}$ yöneyleri için,

Sayıl ile birleşme: $r(s mathbf{a})=(rs)mathbf{a}$
Sayıl toplaması üzerine dağılma: $(r+s)mathbf{a}=rmathbf{a}+smathbf{a}$
Yöney toplamı üzerine dağılma: $r(mathbf{a}+mathbf{b})=rmathbf{a}+rmathbf{b}$
Sayıl birim öğe ile çarpma: $1mathbf{a}=mathbf{a}$

özellikleri sağlanır.

Genel olarak yöneyle sayılın çarpması, yöneyin her bileşeninin sayıl ile çarpılmasıdır.

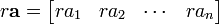
$rmathbf{a}=begin{bmatrix} r a_1 & r a_2 & cdots & r a_n end{bmatrix}$

Nokta (sayıl) çarpım

İki yöney sayıl çarpımla çarpılırsa bir yöney değil bir skaler (sayıl) elde edilir.

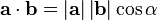
$mathbf{a}cdotmathbf{b} = left|mathbf{a}right|left|mathbf{b}right|cosalpha$

Yöneyleri birim yöneylerle ifade edip, çarpımı birim yöneylerin çarpımından tanımlamak da mümkündür.

$mathbf{a}cdotmathbf{b} = left(a_1 mathbf{e}_1 + a_2 mathbf{e}_2 + cdots + a_n mathbf{e}_n right)cdotleft(b_1 mathbf{e}_1 + b_2 mathbf{e}_2 + cdots + b_n mathbf{e}_n right)$

Eğer birim yöneyler $mathbf{e}_i$ (i = 1, 2, ..., n) olarak gösterilirse (örneğin üç boyutta $mathbf{i}=mathbf{e}_1$ vs.),

$mathbf{e}_i cdot mathbf{e}_j = delta_{ij}$

Burada $δ i j$ ifadesi, Kronecker delta fonksiyonudur ve i ile j eşitse 1, değilse 0 değerini alır. Örneğin;

$mathbf{i}cdotmathbf{j}=0$

$mathbf{j}cdotmathbf{k}=0$

$mathbf{i}^2=mathbf{i} cdot mathbf{i} = 1$

olur. Bu durumda bir yöneyin nokta çarpımı birim yöneylerin çarpımına indirgenmiş olur:

$mathbf{a}cdotmathbf{b} = a_1 b_1 + a_2 b_2 + cdots + a_n b_n$

Ayrıca bu çarpımı dizeylerle de tanımlayabiliriz:

$mathbf{a}cdotmathbf{b} = a^T b =begin{bmatrix}a_1 \ a_2 \ a_3 end{bmatrix}^T begin{bmatrix}b_1 \ b_2 \ b_3 end{bmatrix}=begin{bmatrix}a_1 && a_2 && a_3 end{bmatrix}begin{bmatrix}b_1 \ b_2 \ b_3 end{bmatrix}= a_1b_1+a_2b_2+a_3b_3$

Çapraz (yönel) çarpım

Üç boyutlu iki yöneyin çapraz çarpımı, bu iki yöneyin tanımladığı düzleme dik üçüncü bir yöneye eşittir.

$mathbf{a}timesmathbf{b} = left|mathbf{a}right| left|mathbf{b}right| sin theta mathbf{n}$

ki burada $mathbf{n}$ her iki yöneye dik olan birim yöneydir. Ayrıca yöneyler satır ya da sütün dizeyler (matris) olarak düşünüldüğünde bu çarpım aşağıdaki gibi tanımlanabiir:

$mathbf{a}timesmathbf{b}$	$=begin{bmatrix}a_1 \ a_2 \ a_3end{bmatrix} times begin{bmatrix}b_1 \ b_2 \ b_3 end{bmatrix}$
$quad$	$=begin{bmatrix}0 & -a_3 & a_2 \ a_3 & 0 & -a_1 \ -a_2 & a_1 & 0 end{bmatrix} begin{bmatrix} b_1 \ b_2 \ b_3 end{bmatrix}$
$quad$	$=begin{bmatrix}a_2b_3 - a_3b_2 \ a_3b_1 - a_1b_3 \ a_1b_2 - a_2b_1 end{bmatrix}$

Yönel çarpım determinant ile de tanımlanabilir:

$mathbf{a}timesmathbf{b}$	$=begin{vmatrix} mathbf{i}_1 && mathbf{i}_2 && mathbf{i}_3 \ a_1 && a_2 && a_3 \ b_1 && b_2 && b_3 end{vmatrix}$
$quad$	$=(a_2b_3 - a_3b_2) mathbf{i}_1 + (a_3b_1 - a_1b_3)mathbf{i}_2 + (a_1b_2 - a_2b_1) mathbf{i}_3$

Dikkat edilirse eğer yöneyler paralelse $frac{a_1}{b_1} = frac{a_2}{b_2} = frac{a_3}{b_3}$ olacağından çarpımın sonucu sıfır yöneyidir.

Doğrudan çarpım (tensör çarpımı)

İki yöneyin doğrudan çarpımının sonucu ne bir yöneydir ne bir skalerdir, bir ikiçtir (dyad).

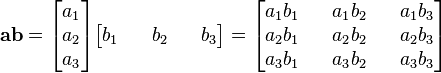
$mathbf{a} mathbf{b} = begin{bmatrix}a_1 \ a_2 \ a_3end{bmatrix} begin{bmatrix}b_1 && b_2 && b_3 end{bmatrix} = begin{bmatrix}a_1 b_1 && a_1 b_2 && a_1 b_3 \a_2 b_1 && a_2 b_2 && a_2 b_3 \a_3 b_1 && a_3 b_2 && a_3 b_3 end{bmatrix}$

Bu çarpıma, eğer yöneyler eş boyutluysa, çiftli (dyadic) çarpım denir. Eğer yöneyleri birim yöneylerle ifade edersek

$mathbf{a}=a_1 mathbf{i}_1+a_2mathbf{i}_2+a_3 mathbf{i}_3$

$mathbf{b}=b_1 mathbf{i}_1+b_2mathbf{i}_2+b_3 mathbf{i}_3$

şeklinde tanımlanan iki yöney için doğrudan çarpım

$mathbf{a} mathbf{b} ,$	=	$( a_1 mathbf{i}_1+a_2mathbf{i}_2+a_3 mathbf{i}_3 ) ( b_1 mathbf{i}_1+b_2mathbf{i}_2+b_3 mathbf{i}_3 )$
	=	$a_1 b_1 mathbf{i}_1mathbf{i}_1 + a_1 b_2 mathbf{i}_1mathbf{i}_2 + a_1 b_3 mathbf{i}_1mathbf{i}_3$
	+	$a_2 b_1 mathbf{i}_2mathbf{i}_1 + a_2 b_2 mathbf{i}_2mathbf{i}_2 + a_2 b_3 mathbf{i}_2mathbf{i}_3$
	+	$a_3 b_1 mathbf{i}_3mathbf{i}_1 + a_3 b_2 mathbf{i}_3mathbf{i}_2 + a_3 b_3 mathbf{i}_3mathbf{i}_3$

olarak elde edilir. Buradaki $mathbf{i}_1mathbf{i}_2$ gibi birimler yeni birer birimdir, yâni başka bir $mathbf{i}$ cinsinden ifade edilemez. Bu yüzden $mathbf{i}_{ij}=mathbf{i}_imathbf{i}_j$ olarak tanımlandığında

$quad$	=	$a_1 b_1 mathbf{i}_{11} + a_1 b_2 mathbf{i}_{12} + a_1 b_3 mathbf{i}_{13}$
	+	$a_2 b_1 mathbf{i}_{21} + a_2 b_2 mathbf{i}_{22} + a_2 b_3 mathbf{i}_{23}$
	+	$a_3 b_1 mathbf{i}_{31} + a_3 b_2 mathbf{i}_{32} + a_3 b_3 mathbf{i}_{33}$

elde edilir ki bu da dizey gösterimine tekâbül eder.