WEBMATEMATİK MATEMATİK SİTENİZ...

Tanım

Dizey, çeşitli şekillerde tanımlanabilir. Örneğin en basit şekliyle bir dizey, sayı tablosudur. Ancak daha tutarlı ve soyut (genel) bir tanım yapılması gerekirse, dizeyi bir sayı dizisi kümesi olarak düşünebiliriz.

A i

, m terimli diziler olmak üzere bir dizey,

{A 1, A 2,..., A n}

sıralı kümesi olarak düşünülebilir.

Daha açık olarak dizeyleri, bileşenleri yöney (vektör) olan bir yöney (vektör) olarak düşünebiliriz.

B i

'ler, m boyutlu yöneyler olmak üzere $vec A=left(vec B_1, vec B_2, ...,vec B_n right)$ yöneyi bir dizey olarak tanımlanabilir.

Tensörlerle ilişkili olacak genellikte tanımlamak istersek, bir dizey biri sütun biri kolon yöney olmak üzere iki yöneyin doğrudan çarpımıdır.

v i

, n boyutlu bir yandeğişken (kovaryant) yöney ve

w j

de m boyutlu bir karşıdeğişken (kontravaryant) yöney olmak üzere bir dizeyin her bir bileşeni $a_i^j=v_i w^j$ olarak tanımlanır. Burada Einstein toplam uzlaşımı kullanılmıştır. Dizeyin tam n.m tane bileşeni olduğu görülür. Eğer sadece dizeylerden bahsediyorsak, $a_i^j$ yerine

a i j

gösterimi yeğlenir.

Cebirsel işlemler

Matematikte çarpma ile çarpım farklı kavramlardır. Çarpma bir ikili işlemdir üstelik kapalıdır. Çarpım ise bir daha genel olarak bir göndermedir. Aynı şekilde toplama ile toplam karıştırılmamalıdır.

Dizey toplaması

Ana madde: Dizey Toplaması

Dizeyler bileşenleri karşılıklı olarak toplanırlar.

c i j = a i j + b i j

Örnek:

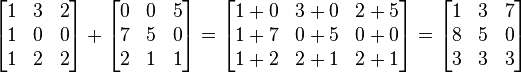
$begin{bmatrix} 1 & 3 & 2 \ 1 & 0 & 0 \ 1 & 2 & 2 end{bmatrix} + begin{bmatrix} 0 & 0 & 5 \ 7 & 5 & 0 \ 2 & 1 & 1 end{bmatrix} = begin{bmatrix} 1+0 & 3+0 & 2+5 \ 1+7 & 0+5 & 0+0 \ 1+2 & 2+1 & 2+1 end{bmatrix} = begin{bmatrix} 1 & 3 & 7 \ 8 & 5 & 0 \ 3 & 3 & 3 end{bmatrix}$

Sayılla (Skalerle) Çarpma

Bir dizey, bir sayıyla çarpılırsa her bileşeni o sayıyla çarpılır.

c i j = k a i j

Örnek:

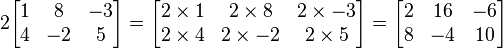
$2 begin{bmatrix} 1 & 8 & -3 \ 4 & -2 & 5 end{bmatrix} = begin{bmatrix} 2times 1 & 2times 8 & 2times -3 \ 2times 4 & 2times -2 & 2times 5 end{bmatrix} = begin{bmatrix} 2 & 16 & -6 \ 8 & -4 & 10 end{bmatrix}$

Dizey çarpımı

Ana madde: Dizey Çarpımı

Dizey çarpımının algoritması ilk öğenin i. satırı, ikinci öğenin j. sütunuyla bileşenleri karşılıklı olarak çarpılıp toplanır ve sonuç dizeyin bileşeni olarak yazılır.

A, mxn boyutlu B de nxs boyutlu dizeyler olmak üzere mxs boyutlu sonuç dizey

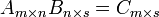
$A_{m times n}B_{n times s} = C_{m times s}$

olarak tanımlanır ve her öğesi

$c_{ij}=sum_{k=1}^{n} a_{ik} b_{kj}$

ile bulunur.

Örnek

$begin{bmatrix} 1 & 0 & 2 \ -1 & 3 & 1 \ end{bmatrix} begin{bmatrix} 3 & 1 \ 2 & 1 \ 1 & 0 end{bmatrix} = begin{bmatrix} (1 times 3 + 0 times 2 + 2 times 1) & (1 times 1 + 0 times 1 + 2 times 0) \ (-1 times 3 + 3 times 2 + 1 times 1) & (-1 times 1 + 3 times 1 + 1 times 0) \ end{bmatrix} = begin{bmatrix} 5 & 1 \ 4 & 2 \ end{bmatrix}$

Çarpmayı, ilk öğenin her satırını bir yöney ve ikinci öğenin her sütununu bir yöney olarak düşünüp ilk öğeyi bir sütun yöney ve ikinci öğeyi bir satır yöney olarak yöney iç çarpımına indirgeyebiliriz. Örneğin, $vec{a}$ ve $vec{b}$ yöneyleri n boyutlu olmak üzere,

$A_{m times n}=begin{bmatrix} vec{a_1} \ cdots \ vec{a_m} end{bmatrix}$ ve $B_{n times s}=begin{bmatrix} vec{b_1} && cdots && vec{b_s} end{bmatrix}$

şeklinde düşünüldüğünde çarpım,

$A B = begin{bmatrix} vec{a_1} cdot vec{b_1} && cdots && vec{a_1}cdotvec{b_s} \ vdots && ddots && ddots \ vec{a_m}cdotvec{b_1} && cdots && vec{a_m}cdotvec{b_s} end{bmatrix}$

biçimini alır. Bu şekilde düşünmek kağıt üzerinde dizeyleri çarparken işe yarayabilir ve zaman kazandırır.

Örnek

$begin{bmatrix} 3 & 0 \ -1 & 2 end{bmatrix} begin{bmatrix} 7 & -1 \ 3 & 6 end{bmatrix}$	$= begin{bmatrix} (3,0) \ (-1,2) end{bmatrix} begin{bmatrix} (7,3) & (-1,6) end{bmatrix}$
	$= begin{bmatrix} (3,0)cdot(7,3) && (3,0)cdot(-1,6) \ (-1,2)cdot(7,3) && (-1,2)cdot(-1,6) end{bmatrix}= begin{bmatrix} 21 && -3 \ -1 && 13 end{bmatrix}$

Kronecker (Doğrudan) toplam :

Ana madde: Doğrudan Toplam

Bu toplamın sonucu bir dizeyler köşegenidir.

$C=oplus_{i=1}^{k} A_i=text{kosegen}left( A_1,A_2,...,A_k right)=left[ begin{array}{cccc} A_1 & 0 & cdots & 0 \ 0 & A_2 & cdots & 0 \ vdots & vdots & ddots & vdots \ 0 & 0 & cdots & A_k \ end{array} right]$

burada sonuç dizeyin boyutları, toplanan dizeylerin doğrudan boyutları toplamı kadardır.

Kronecker (Doğrudan) çarpım : [değiştir]

Ana madde: Doğrudan Çarpım

Bu çarpım ilk öğenin her bileşenini ikinci öğeyle doğrudan çarpmayla tanımlanır.

$A_{m times n} otimes B_{r times s} = left[ begin{array}{cccc} a_{11}B & a_{12}B & cdots & a_{1n}B \ a_{21}B & a_{22}B & cdots & a_{2n}B \ vdots & vdots & ddots & vdots \ a_{m1}B & a_{m2}B & cdots & a_{mn}B \ end{array} right]$

buradan,

$C_{(m r) times (n s)}=left[ begin{array}{ccccc} a_{11}b_{11} & a_{11}b_{12} & cdots & a_{12}b_{11} & cdots \ a_{11}b_{21} & a_{11}b_{22} & cdots & a_{12}b_{21} & cdots \ vdots & vdots & ddots & quad & quad \ a_{11}b_{11} & a_{21}b_{12} & quad & ddots & quad \ vdots & vdots & quad & quad & ddots \ end{array} right]$